Measuring Noise
Cities are noisy places — I know, because I live in the middle of one — but what is unreasonable noise? That was the question I wanted to try and answer for residents of a nearby street who were being woken up in the early mornings by the noise of buses leaving a depot to reach the start of their routes. I had to find a way to measure noise to a reasonably high standard using cheap and relatively simple equipment, but that turned out to be the easy bit. Much more difficult was then understanding what I had measured and demonstrating what it meant. I’m think I’ve succeeded, at least in part, but read on and see what you think!
What is noise?
At a physical level, sound is simply pressure waves travelling through a fluid (air or water). When those pressure waves reach us, they are converted into nerve signals by the structures in our ears, and our brains interpret those signals into what we experience as sounds. Human ears have an amazing range of sensitivity — there is roughly a million times difference in sound pressure between the quietest sounds that we can hear and the loudest sounds at the threshold of pain. As well as the magnitude of the pressure waves, our ears can sense their frequency and also the direction they are coming from, allowing us to experience the soundscape around us in exquisite detail. But beyond those purely physical aspects, the interpretation of sounds by our brains creates a more subjective experience. Sounds can sooth or startle, be pleasurable or painful, attract or annoy.
The word “noise” usually means a sound that causes a person irritation in some way, but that definition still allows for a broad range of interpretation. Irritating sounds can be quiet (a dripping tap) or loud (a backfiring car exhaust), they can vary in frequency (the high-pitched whine of a fan or the thumping bass from a nightclub), they can be continuous (the roar of a nearby motorway) or intermittent (passing cars on a quiet street). Whether or not a particular sound negatively affects a person can depend on who they are, what they are expecting, how close the sound is, and even what time of day it is. A sudden sound in the dead of night might be enough to wake someone up, while that same person might not even notice an identical sound during the daytime.
Finding a way to wrap all that complexity up into a single definition of “noise” and then measure it might seem like an impossible task, but in the early 2000s the European Union decided to try …
The END of noise
In response to a World Health Organisation report about the negative health impacts of noise, the European Parliament passed the Environmental Noise Directive (END). This required member states to consider the impacts of noise on people and take steps to mitigate those impacts where they were excessive. It created a framework for how authorities should determine, communicate and reduce the effects of environmental noise. In Scotland, the result was a website, Scotland’s Noise, which maps the expected noise levels in the main population centres (“agglomerations”) across the country. Here’s what it looks like for central Edinburgh, where I live:
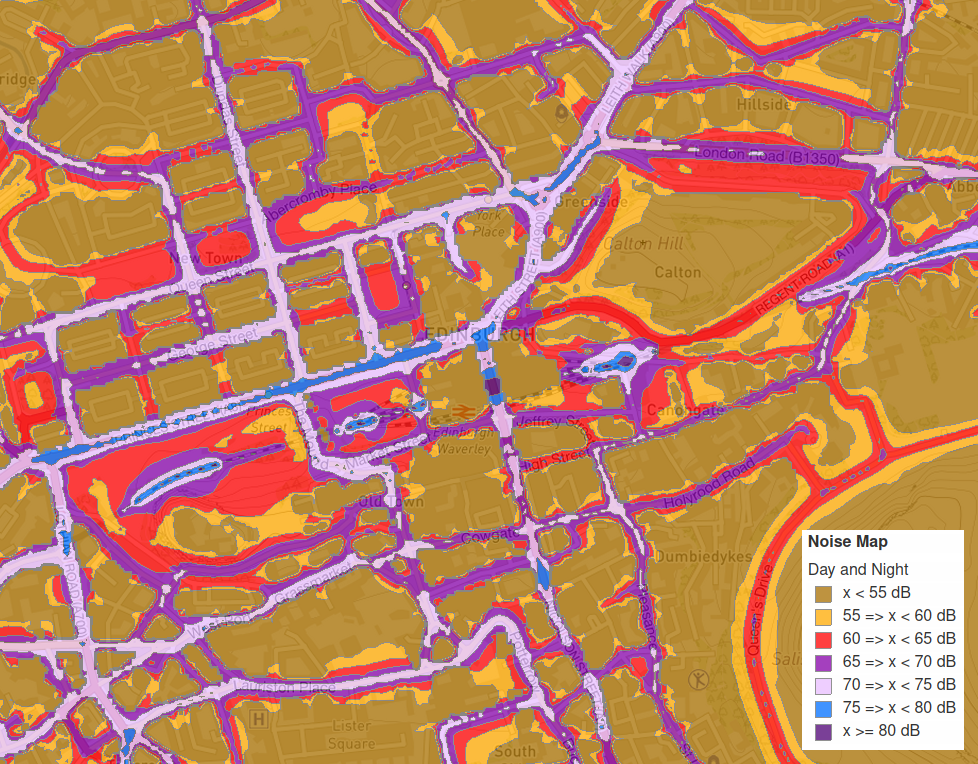
My home lies in a red-shaded area of the map, so it looks like I should experience noise levels of between 60 and 65 dB, but what does that actually mean? Well, the FAQ section of the website does a pretty good job of explaining how they made the map. They did not send out an army of people to measure sound levels on every street corner over a long period! Instead, they fed existing data on things like traffic, public transport, industrial sites, building locations and population density into a mathematical model that would predict the expected environmental noise level at any point. The model divided the area up into 10m squares and predicted Leq (equivalent continuous sound pressure level) at a point 4m above the ground in the centre of each of those squares. The noise contours on the map are then calculated from those predictions.
The main map above shows the average noise levels throughout the day and night. There is also a separate map that shows just the night-time noise levels:
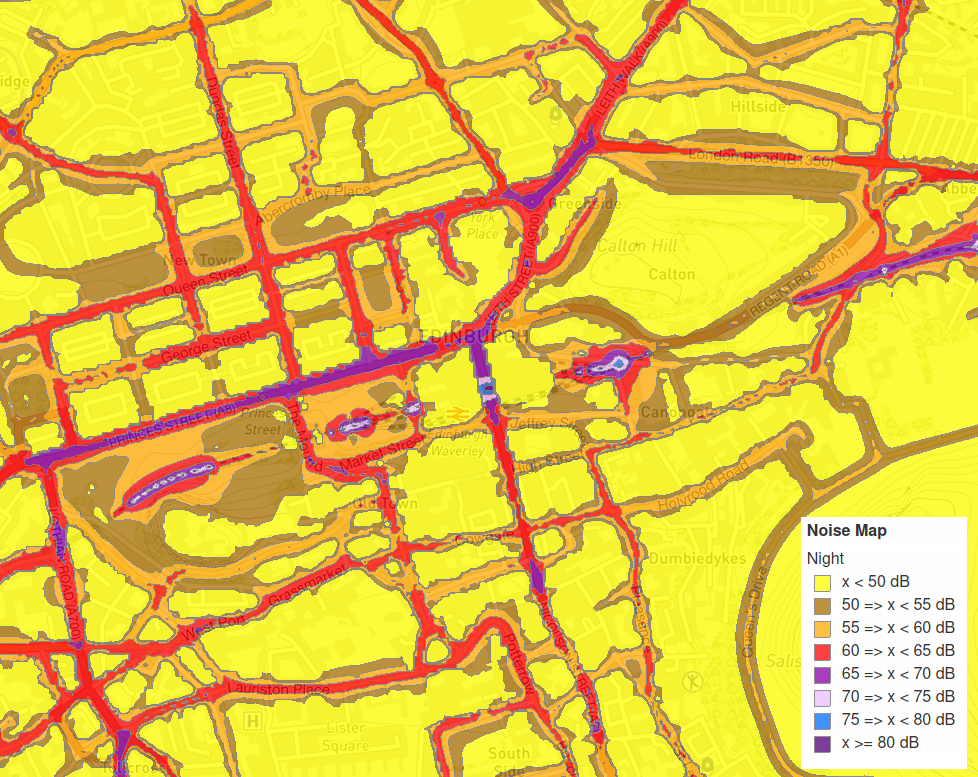
So the maps show the average typical noise levels I should expect to experience in a particular location (provided I happen to be floating 4m above ground level, of course). That’s relatively straightforward, but how useful are they?
This next bit gets rather mathematical, so feel free to skip past it if you’re not that way inclined, but it does help to explain why thinking about sound levels is not straightforward.
What the L?
First, I need to fully understand how sound pressure levels are defined. The sound pressure level (Lp) at any moment is expressed as a ratio of the pressure at that moment(P) with a baseline pressure level (P0):
For noise measurement purposes, P0 is taken to be 20 \(\mu Pa\), which is about the lowest pressure level that human ears can detect. I mentioned before that the human ear can deal with sound pressure levels varying by a million times between the quietest and loudest sounds, so this pressure ratio can be anywhere from 1 to 1,000,000 or more.
People don’t really cope well with large number ranges, so sound pressure ratios are usually converted to a logarithmic form (L) measured in Bels (B — named in honour of Alexander Graham Bell). On that scale, 0 B is the quietest sound a human can detect, while 12 B is getting painfully loud. For some reason, it was then decided that Bels were too big and it was better to express measurements in tenths of a Bel, or deciBels (dB):
Here are some examples of approximate sound levels:
| Sound | Pressure | Bels | deciBels |
|---|---|---|---|
| Threshold of hearing | 0.00002 Pa | 0 B | 0 dB |
| Leaves rustling, whispering | 0.0002 Pa | 2 B | 20 dB |
| Quiet room | 0.002 Pa | 4 B | 40 dB |
| Normal conversation | 0.02 Pa | 6 B | 60 dB |
| Heavy traffic | 0.2 Pa | 8 B | 80 dB |
| Motorbike | 2 Pa | 10 B | 100 dB |
| Rock concert | 20 Pa | 12 B | 120 dB |
| Balloon popping | 200 Pa | 14 B | 140 dB |
| Jet engine | 2000 Pa | 16 B | 160 dB |
Raising L
While the logarithmic dB scale makes the numbers easier to write down, it ends up making calculations using dB measurements much more difficult. You can’t simply add, subtract, multiply or average dB values. To appreciate why, consider a car passing you on a quiet road – the noise it makes might reach, say, 80 dB as it goes past. Now consider what happens if another car passes you in the opposite direction at the same time. Is the noise level \(80 + 80 = 160 dB\)? That is the noise equivalent of standing right next to a jet engine, which is clearly not comparable!
To do any calculations with decibels, you first have to convert them into sound pressure ratios, perform your calculation, and then convert the result back into decibels again. So in the passing cars example above, if the sound levels from the two cars are called L1 and L2 the calculation would be:
What a palaver! Nevertheless, you can see that the sound level of two 80 db noises added together is only slightly larger, at a more realistic 83 dB, and not the overestimate of 160 dB you get from simply adding the dB values together.
The same thing is true if you want to average a series of sound level measurements taken over a time period. A simple arithmetic mean of decibel values isn’t useful because of the logarithmic scale, so instead you need to calculate Leq or the “equivalent continuous sound level”, by converting all the decibel values to sound pressure ratios, averaging them, and then converting the result back into a decibel value again. For a series of n measurements, L1 to Ln:
Leq is the closest you can get to an “average” sound level — it is the theoretical constant sound level that would create the same total sound pressure as the actual variable measurements taken over the sample period. Strictly speaking, you also need to specify the time period over which the measurements have been taken, so, for example, Leq,1h is the equivalent continuous sound level over a sample period of 1 hour.
One L of a day
The Environmental Noise Directive promotes the use of a statistic called LDEN which is designed to encapsulate the effects of noise over a whole day. It is made up of three Leq measurements over different daily time periods, which have different “penalties” assigned to them:
| Start | End | Duration | Penalty | |
|---|---|---|---|---|
| Lday | 07:00 | 19:00 | 14 hours | +0 dB |
| Levening | 19:00 | 23:00 | 4 hours | +5 dB |
| Lnight | 23:00 | 07:00 | 8 hours | +10 dB |
Once again, we have to do the same logarithmic conversions when calculating LDEN, so the full formula looks like this:
Finally I have a single number that is supposed to express the level of environmental noise in a particular location over the course of a whole day. In fact, the first of the noise maps that I included earlier shows the predicted LDEN levels for different locations, while the second map does the same for Lnight levels only. To check if the map is realistic for any location, I just need to make three measurements of noise over different daily time periods and feed them into this formula.
Practical noise measurement on a budget
Professional integrating sound pressure level meters, that can log noise levels over time to measure Leq, cost many hundreds or even thousands of pounds — well beyond the means of my simple project. Much cheaper, simpler devices are available that can give reasonably accurate spot measurements of noise levels, and I was able to modify one of these to allow me to log the measurements over time. The full details of the “PicoDeeBee” meter will be available on my GitHub page, but in essence it is a cheap, generic model of decibel meter adapted to provide an output to a tiny microcontroller that records the timestamped data to a spreadsheet file which can be downloaded over USB. The total cost of the components is about 35 GBP.
The sound meter measures A-weighted (i.e. tuned to the same frequency sensitivity as the human ear) sound pressure levels and converts them to decibel readings at a rate of 6 times per second. These decibel levels are output as a voltage which is detected and recorded by the microprocessor. Because of limited storage space, I’ve programmed the microprocessor to calculate the equivalent continuous sound level from the combined individual readings over the course of a minute, and save Leq,1 min measurements to the data file. It also records the maximum and minimum sound readings, Lmax and Lmin, for each minute. A battery-powered clock ensures that the timestamps of each measurement are reasonably accurate. Set up like this, the meter can be left running for days or weeks at a time before the data are copied off and analysed.
For testing, I simply set up PicoDeeBee next to an open window in my flat and left it running for about two weeks to record the noise levels on my street. Since my flat is on an upper floor, the position of the meter roughly matched the 4m height used in the noise mapping, and so it should enable a useful comparison with with the modelled data.
Looking at the test data
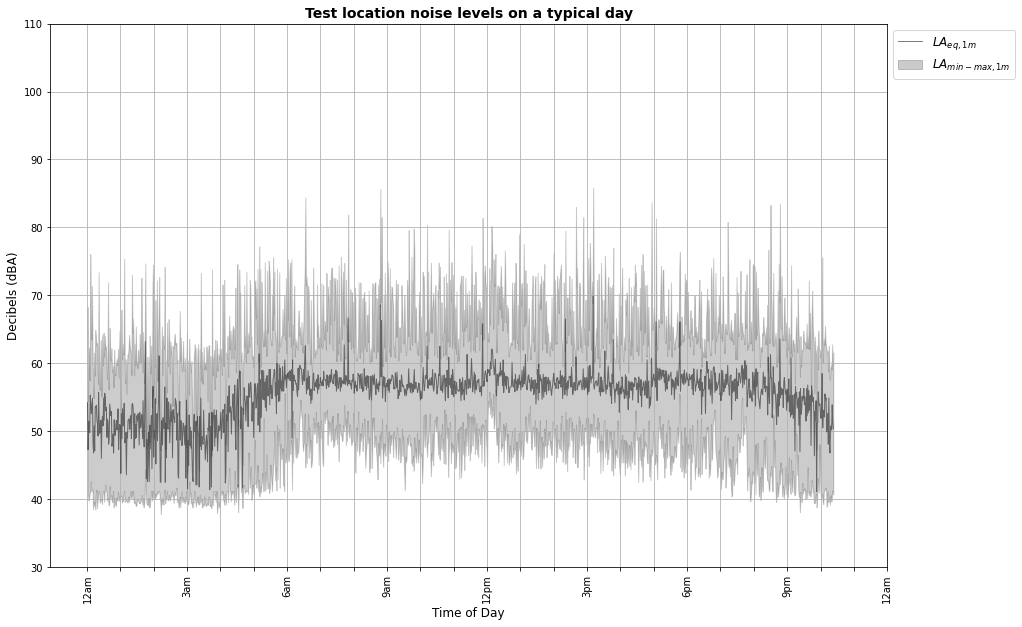
Above is a plot of a typical weekday’s data. The dark line is Leq,1 min, the average sound level recorded each minute, while the grey area behind it shows the range of minimum and maximum sound levels in the same period.
The main thing to notice is how … er … “noisy” it is. The sound levels vary quite widely over time, even when averaged over minute-long periods. The minimum and maximum sound levels for each minute are also very variable. Now have a look at the next plot:
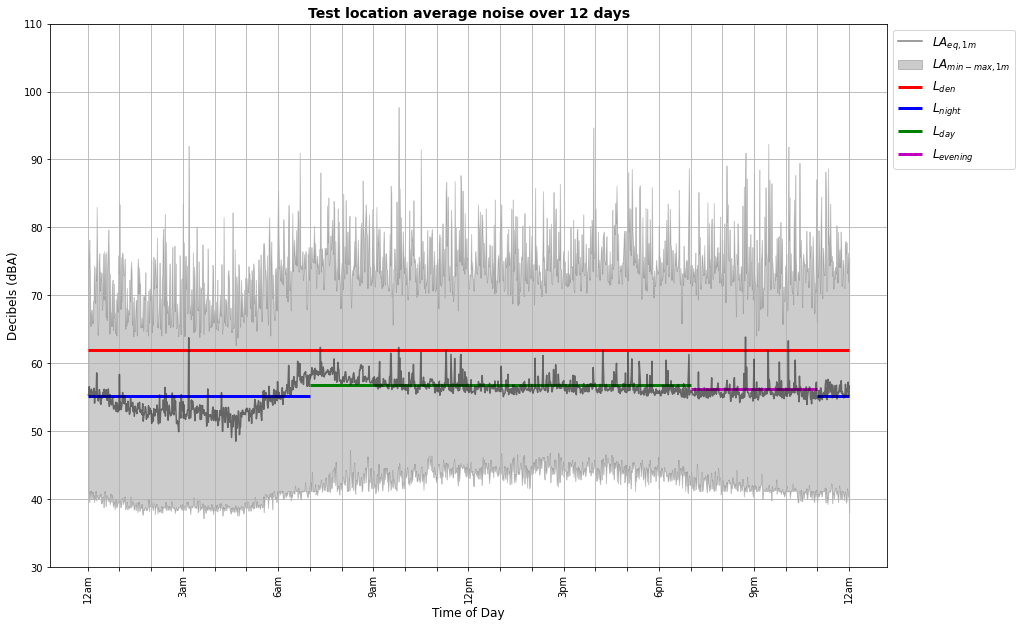
This is 12 day’s worth of data combined and summarised using the techniques described above. The Leq,1 min line still has a fair bit of variation, but it is now possible to pick out some general trends: the relative quiet of the early morning is lost from around 5am onwards as the traffic of the morning rush-hour rises to a peak between 7-8am and then the noise level stays relatively steady through the rest of the day before tailing off slightly in the late evening. Nevertheless, these changes are fairly modest — the noise level stays broadly within the same small range of values throughout the whole day and night.
The coloured horizontal lines on the graph show the corresponding Lday, Levening, and Lnight values calculated from the data, as well as the combined LDEN measurement used in the END mapping. Here are the exact figures:
| Measured | Predicted | |
|---|---|---|
| Lday | 56.9 dB | |
| Levening | 56.2 dB | |
| Lnight | 55.3 dB | 55-60 dB |
| LDEN | 62.0 dB | 60–65 dB |
It’s interesting to see how the combined LDEN figure is more than 5dB higher than the actual daytime noise level. This rather artificial inflation of the combined figure over its measured components is due to the penalties for evening and night-time noise that are applied in the LDEN calculation, and can seem rather counter intuitive. It will happen anywhere there is relatively little variation between the daytime and night-time noise levels.
The noise maps of Edinburgh predict that I should experience an LDEN of 60–65 dB and an Lnight of 55–60 dB, which turn out to be pretty accurate estimates of the actual noise levels at my location.
Losing the bin lorry in the haystack
Most mornings, at some time between 6am and 7am, there is a noisy lorry that comes along my street to empty rubbish bins. It wakes me up so often, I’ve started calling it my morning Reveille. If I can demonstrate the effect of the morning bin lorry in the test data, then I should be able to do the same for the residents I want to help on the bus-blighted street.
Well, looking at the graphs above, can you spot the bin lorry noise?
No, I can’t either.
The huge amount of minute-to-minute variation in the Leq values swamps any daily trends, and hides the specific noise events I’m looking for. Unfortunately, even looking at the minimum and maximum sound levels doesn’t really help. The Lmin levels show that the noise floor is definitely quieter at night, but what is perhaps surprising is how high the Lmax levels can be right through the nighttime and early morning. Noise events of 80 and even 90 dB can apparently happen at any time of night and yet somehow I manage to sleep through them! I still can’t see the effect of the bin lorry that actually wakes me up, though.
So if I can’t even spot the bin lorry in my test data, how will I be able to demonstrate the effects of the passing buses for the bleary-eyed people in the street nearby? Well, I thought I would give it a try anyway.
Sounding out the street
Here is a chart of the data from the sample location on the neighbours’ street. The data were collected in the same way and over a similar time period to my test data:
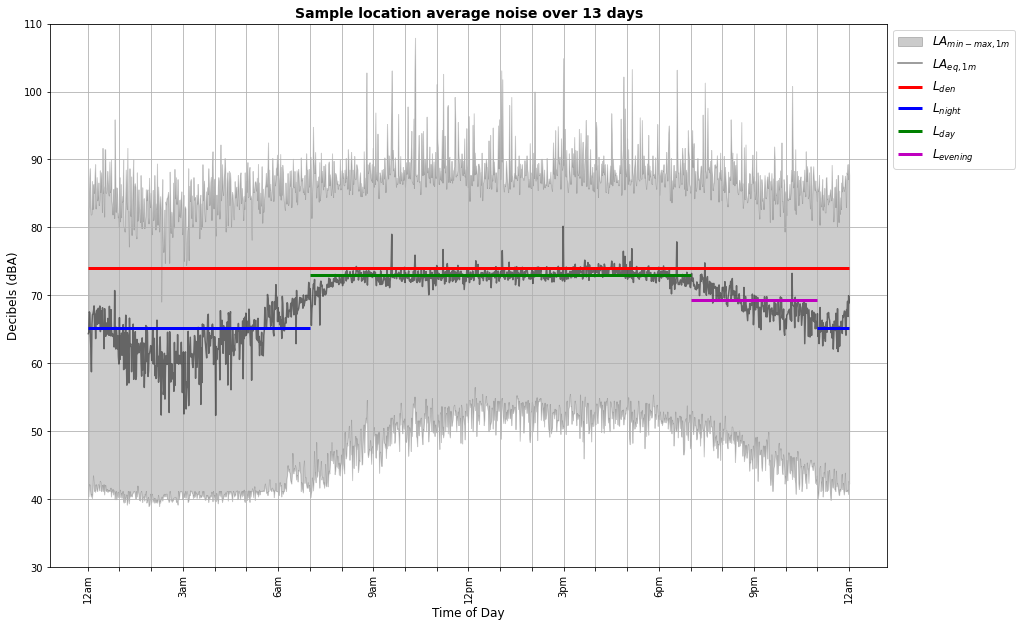
| Measured | Predicted | |
|---|---|---|
| Lday | 73.0 dB | |
| Levening | 69.4 dB | |
| Lnight | 65.2 dB | 55-60 dB |
| LDEN | 74.1 dB | 65–70 dB |
While the broad shape of the graph is similar to my test data, the most striking thing to notice is the generally higher levels of noise throughout the day and night. It is at least 10 dB louder at any time of day than in my own location, which — bearing in mind the logarithmic nature of deciBel values — makes it a much noisier street. No wonder the residents there are upset!
Looking at the graph in more detail, you can see that daytime average noise levels are consistently above 70 dB between 7am and 9pm. The minimum sound level rarely drops below 50 dB and the maximum can sometimes go above 100 dB during the day. Even at night, the average sound level stays well above 60 dB and there are frequent maxima of 85–90 dB. However, there is a greater absolute change in noise levels between day and night than in my test data, which means that the overall LDEN is not so much higher than the actual daytime noise level — the artificial penalties added to evening and night-time noise don’t end up exaggerating the combined figure as much as they do at my own location.
Missing the bus but getting there in the END
A particular issue at the sample location is apparently the noise from early morning convoys of buses leaving a nearby depot to start their daytime services. Thirty or forty buses rumble down the street every day between about 4am and 7am, causing a significant noise nuisance for residents trying to get a good night’s sleep. Unfortunately, the data I’ve collected don’t really demonstrate this effect. The average noise level gradually increases throughout the early morning, just as it does at my own location — there’s no obvious sign of the increased nuisance from the passing buses.
I’m not really sure why that is, but it may be something to do with the way my sound meter averages sound levels over 1-minute intervals: each bus will take much less than a minute to go past, so perhaps the resolution isn’t fine enough to pick out these individual noise events. Nevertheless, I would have thought that the cumulative noise of so many passing buses would have had a more obvious overall effect on the data.
There is still plenty of cause for concern, though. The World Health Organisation produced updated guidance for European environmental noise levels in 2018, and to quote from the executive summary:
For average noise exposure, the Guideline Development Group (GDG) strongly recommends reducing noise levels produced by road traffic below 53 decibels (dB) LDEN , as road traffic noise above this level is associated with adverse health effects.
For night noise exposure, the GDG strongly recommends reducing noise levels produced by road traffic during night time below 45 dB Lnight , as night-time road traffic noise above this level is associated with adverse effects on sleep.
To reduce health effects, the GDG strongly recommends that policy-makers implement suitable measures to reduce noise exposure from road traffic in the population exposed to levels above the guideline values for average and night noise exposure. For specific interventions, the GDG recommends reducing noise both at the source and on the route between the source and the affected population by changes in infrastructure.
The measured values of 74.1dB LDEN and 65.2 dB Lnight at the sample location are very much higher than these recommended limits, and they are even well above the ranges predicted by the Scotland’s Noise maps. So my data strongly suggest that the residents on this street are likely to be suffering significant adverse health effects due to environmental noise. Local authorities may have underestimated the strength of these health effects, because of the difference between the predicted and actual noise values.
I very much hope that this simple study will prompt further investigations into the causes of the high environmental noise levels and lead to solutions that can finally provide the residents with some relief!